这是一个创建于 2975 天前的主题,其中的信息可能已经有所发展或是发生改变。
现在有一个存放了 n 个线段(起点和终点坐标)的数组,结构如下:
[
[(sx_1,sy_1),(ex_1,ey_1)],
[(sx_2,sy_2),(ex_2,ey_2)],
......
[(sx_n,sy_n),(ex_n,ey_n)]
]
有没有这样一个,以其中某个点为起点,走过所有线段,并且使得总的行程最短的算法?
这里的距离不仅包含线段的长度,还包含线段之间的跳转距离。
要求就是:走线段的时候,必须从线段一端进入,从另一端退出,且不能有重复走某条线段。
[
[(sx_1,sy_1),(ex_1,ey_1)],
[(sx_2,sy_2),(ex_2,ey_2)],
......
[(sx_n,sy_n),(ex_n,ey_n)]
]
有没有这样一个,以其中某个点为起点,走过所有线段,并且使得总的行程最短的算法?
这里的距离不仅包含线段的长度,还包含线段之间的跳转距离。
要求就是:走线段的时候,必须从线段一端进入,从另一端退出,且不能有重复走某条线段。
第 1 条附言 2017 年 12 月 27 日 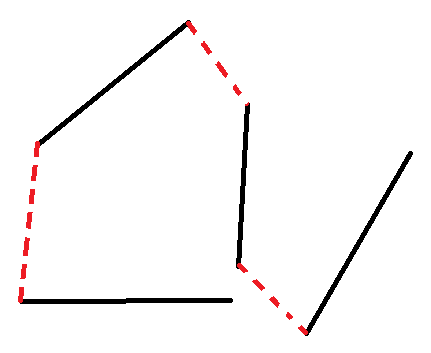

如图,黑色代表的是需要走过的线段,红色的是跳转线路; 现在就是有这些线段的起始点和终止点的坐标,需要求出一条路径来,使得红色的跳转距离最短(也就是总行程最短)。
随意画了个图,意思一下就好了。
1 zjp 2017 年 12 月 27 日 via Android 可以转化为图的问题。并不能保证某个点可以到达所有边(不连通),也不能保证不重复走(有死端) |
2 hinate 2017 年 12 月 27 日 这是类似走迷宫吗? |
3 ynyounuo 2017 年 12 月 27 日 这不是 MST ? |
4 ynyounuo 2017 年 12 月 27 日 好吧,并不一样。 |
5 zj299792458 2017 年 12 月 27 日 听起来是遍历所有点,直接深度优先搜索 |
6 ynyounuo 2017 年 12 月 27 日 感觉比较类似 TSP 问题,可以去参考一下 |
7 aheadlead 2017 年 12 月 27 日 我觉得以后提问的时候最好多画几张图 也便于别人看懂意思 |
8 ladeo 2017 年 12 月 27 日 via Android ospf |
10 geelaw 2017 年 12 月 27 日 via iPhone 什么是“线段之间的跳转距离”? |
11 xinhangliu 2017 年 12 月 27 日 via Android 模拟退火 |
12 Bryan0Z 2017 年 12 月 27 日 via Android MST 的算法改一下? |
14 luoshuangfw 2017 年 12 月 27 日 via Android 需要明确一下:从一条边的 end 出来,是否可以进入剩下所有边中任意一条边的 start,只要没走过? |
17 elfive OP @luoshuangfw 只要保证:1、走过所有线段; 2、不重复走任何一条线段; 3、线段不能拆分,这 3 个条件就 OK 了 |
18 Bryan0Z 2017 年 12 月 27 日 via Android 找一个线段当起点 依次判断其他线段端点到它的端点的距离,找到一个最小的加入 重复步骤二 反正就那个意思,把 prim 或者 d 算法改一下就好了 |
19 Bryan0Z 2017 年 12 月 27 日 via Android 哦,不太一样 |
20 luoshuangfw 2017 年 12 月 27 日 @Bryan0Z 这是不行的,不是 MST ;确切的说要求的不是一棵树,而是一个回路 |
21 wafm 2017 年 12 月 27 日 曾经干游戏的时候做过一个类似的玩意 我提供一条思路 比如你说的图,如果从黑线的一端走到另一端,确定到达端点后,原地做一个半径算法,半径最短的黑点取点,再判断哪个点最优。 |
22 Bryan0Z 2017 年 12 月 27 日 via Android @luoshuangfw 再加一个条件,一旦连完,把那两个端点删掉就好了,基本思路肯定不会有问题 |
23 luoshuangfw 2017 年 12 月 27 日 @Bryan0Z 这是不行的,树的端点(也就是叶子)有许许多多个,你到达叶子之后准备往哪里走? |
24 xingwing 2017 年 12 月 27 日 bitmap |
25 geelaw 2017 年 12 月 27 日 这个问题是 NP-困难的考虑一个特殊情况,就是每个线段的长度都是 0 的时候。 https://en.wikipedia.org/wiki/Travelling_salesman_problem#Euclidean_TSP |
26 luoshuangfw 2017 年 12 月 27 日 @geelaw 我一开始也想到 TSP,但不知道咋 reduction 蓝后看到你这个,才知道原来 Euclidean TSP 也是 NP-Hard= = |
27 Vinty 2017 年 12 月 27 日 其实就是 tsp 问题啊,只不过原始 tsp 中是点,这里换成了线段而已,线段会多一个出入方向的二元参数, 不过即使这类问题最常用的元启发算法,我自己的使用感受来看,对高维高相关的问题其实效率也是有限,但没办法没什么别的好方法 |
28 Bryan0Z 2017 年 12 月 27 日 via Android @luoshuangfw 很简单呀,生成的树肯定只有两个端点可以试,然后待定线段还有 n 个,无非是试 4n 次,总算法效率 n 方能接受 |
29 Kilerd 2017 年 12 月 27 日 这不就是图的经典算法吗? 把黑边当成图的点,然后存在全链接的图,代价就是距离,然后用最短距离算法就可以算出来了啊 PS:好久没用过了,所以可能名词用得不是很对,所以大概意思懂了就行 |
30 klesh 2017 年 12 月 27 日 最小生成树就行了吧. 由于线都是要走完, 它是不变的, 不用考虑. 唯一变化的就是两条线端点之间的距离. 把这个距离看作权值. 那就是最小生成树了 |
31 arzterk 2017 年 12 月 27 日 NP-Hard 的问题,没有稳定的算法吧 |
33 quinoa42 2017 年 12 月 27 日 粗略的大致思路如下: 0 )为了解题需要建 graph 1 )计算每个线段的长度,把线段长度记为 graph 中每个 node 的权值 2 )对于任意的两条线段 s1, s2,求 s1 两端两点到 s2 两端两点,总共 4 段跳转线段的长度,并保留最短的那条作为 node s1 到 node s2 的 edge 的权值 3 )这样题目的数据就转化成了一个 complete graph,因为要走过每个点,每个 node 的权值和结果无关(这部分永远是要加在一起,加入最短路径里的) 4 )总结:预处理之后实际上是要找到一条路径遍历所有 node 且不重复经过其中一个 node,这个问题是 NP-complete 的,参见 https://en.wikipedia.org/wiki/Hamiltonian_path 5 )具体做法我脑子笨,只能想到一个略暴力的动归:a[s][i][j]表示对于一个 graph 中所有 node 的子集 s,从 node i 到 node j 可得到的最短遍历路径 如果指定起点的话就是 a[s][i],表示在子集 s 中从起点到终点 node i 可找到的最短遍历路径,但不管哪种,枚举 s 需要 O(2^n),500 的数据规模怎么看都不太现实 |
34 gaohongyuan 2017 年 12 月 27 日 楼主的问题的一个特例是:所有的线段长度为 0 也就是旅行商问题 ( TSP )。所以,这个问题比 TSP 更加困难。 因为 TSP 是 NP-Hard 问题,所以楼主的问题也是 NP-Hard 问题,即不存在高效(多项式时间复杂度)的解法。 说错请指正。。 |
35 zzl 2017 年 12 月 27 日 迪杰斯特拉算法???我 GIS 行业中最短距离算法 |
36 quinoa42 2017 年 12 月 27 日 @zzl dijkstra 是用 priority queue,以一个类似广搜的模式寻找一个图中从某节点出发到某节点截止的最短路径,无法保证找到的最短路径遍历了所有节点 |
37 klesh 2017 年 12 月 27 日 @arzterk 这个与 TSP 还是有区别的, 有些线已经被确定, 而且 TSP 是一个回路, 这个需要的是一个通路就够了. 复杂度低很多. 题主请说明下起始点是随机指定的, 求这个路径. 还是点和路径要一起求? |
39 ordog 2018 年 1 月 2 日 添加一个虚拟的起始点 O,O 到所有线段两端的距离相同,比如都是 0。问题转化为一个全联通的 TSP 问题(包括 O 点在内),只是一些两两点之间路径固定(初始的黑色线段)。如果问题规模不大,是可以通过整数规划求精确解的。如果采用一些 tsp 的启发式方法求解,需要注意由于 O 点的存在,两边之和大于第三边的法则这里不适用。 |
